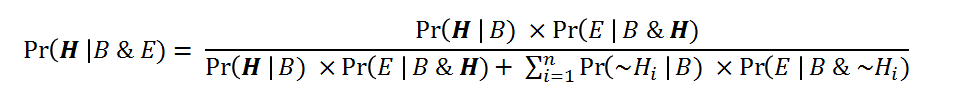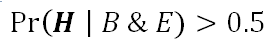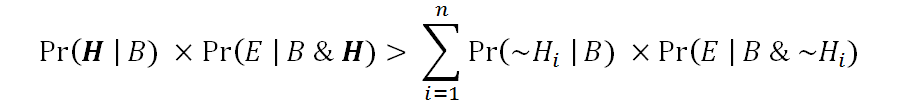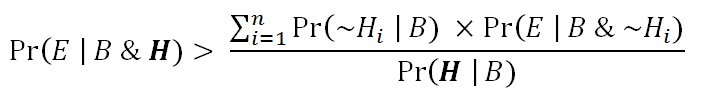(This article was originally published on this blog on June 21, 2012. I am reposting because William Lane Craig recently tweeted a link to a video in which he objects to ECREE.)

In my last post, I offered a Bayesian interpretation of the principle, “extraordinary claims require extraordinary evidence” (ECREE). William Lane Craig, however, disagrees with ECREE. In a response to philosopher Stephen Law, Craig wrote this.

This sounds so commonsensical, doesn’t it? But in fact it is demonstrably false. Probability theorists studying what sort of evidence it would take to establish a highly improbable event came to realize that if you just weigh the improbability of the event against the reliability of the testimony, we’d have to be sceptical of many commonly accepted claims. Rather what’s crucial is the probability that we should have the evidence we do if the extraordinary event had not occurred.3 This can easily offset any improbability of the event itself. In the case of the resurrection of Jesus, for example, this means that we must also ask, “What is the probability of the facts of the empty tomb, the post-mortem appearances, and the origin of the disciples’ belief in Jesus’ resurrection, if the resurrection had not occurred?” It is highly, highly, highly, improbable that we should have that evidence if the resurrection had not occurred.

————

[3] See the very nice account by S. L. Zabell, “The Probabilistic Analysis of Testimony,” Journal of Statistical Planning and Inference 20 (1988): 327-54.

I agree with Craig that it would be incorrect to “just weigh the improbability of the event against the reliability of the testimony.” I also agree with Craig that “the probability that we should have the evidence we do if the extraordinary event had not occurred … can easily offset any improbability of the event itself.” I disagree with Craig, however, regarding his interpretation that ECREE requires that we ignore that probability. This can be seen using Bayes’s Theorem (BT).

Let B represent our background information; E represent our evidence to be explained; H be an explanatory hypothesis, and ~H be the falsity of H. Here is one form of BT:

As I argued in my last post, an “extraordinary claim” is an explanatory hypothesis which is extremely improbable, conditional upon background information alone, i.e., Pr(H | B) <<<  0.5. And “extraordinary evidence” can be interpreted as the requirement that a hypothesis’s explanatory power is proportionally high enough to offset its prior improbability (the “extraordinary claim”). Here I offer an even more precise definition.

It follows from BT that H will have a high epistemic probability on the evidence B and E:

just in case it has a greater overall balance of prior probability and explanatory power than its denial:

Thus, we can somewhat abstractly define “extraordinary evidence” as evidence that makes the following inequality true:

With that inequality in mind, let’s return to Craig’s objection to ECREE. Here again is the relevant portion of his objection:

Probability theorists studying what sort of evidence it would take to establish a highly improbable event came to realize that if you just weigh the improbability of the event against the reliability of the testimony, we’d have to be sceptical of many commonly accepted claims. Rather what’s crucial is the probability that we should have the evidence we do if the extraordinary event had not occurred.

It seems, then, that Craig’s objection to ECREE is based upon an interpretation of ECREE which requires that we only consider the “extraordinary claim,” i.e., Pr(H | B). If that interpretation is correct, then I will join Craig in rejecting ECREE. But is it correct?

In mathematical notation, “the probability that we should have the evidence we do if the extraordinary event had not occurred” is Pr(E | B & ~H). But now consider again the inequality used to define extraordinary evidence.

The expression, Pr(E | B & ~H), is literally right there, in the numerator on the right-hand side. It appears, then, that Craig’s objection is based upon a misinterpretation of ECREE. For the same reason, Craig’s reason that ECREE would cause us “to be sceptical of many commonly accepted claims” is therefore misplaced.

I could be wrong, but I suspect there are two factors which contributed to this misinterpretation. First, many skeptics have used ECREE in connection with (or as support for) Hume’s argument against miracles. While I’m inclined to agree with John Earman that Hume’s argument is highly overrated–i.e., it may be the case that BT does not provide Hume with the support many skeptics think it provides–this is not of obvious relevance to ECREE. ECREE, like BT, is not dependent on Hume.

The other factor which may have contributed to the misinterpretation is the definition of “extraordinary claim;” Craig may disagree with the criteria skeptics have used to determine whether a claim is extraordinary. I think it is helpful to use probabilistic notation to clarify the issue. Again, I proposed that an “extraordinary claim” is an explanatory hypothesis which is extremely improbable, conditional upon background information alone, i.e., Pr(H | B) <<<  0.5. Let’s assume, for the sake of argument, that definition is wrong. Instead, define an “extraordinary claim” as any explanatory hypothesis H which has a prior probability below some number x, i..e., Pr(H | B) < x, where x can be any real number between 0 and 1. Here’s the point. X can be any real number between 0 and 1. It doesn’t matter which value one chooses, since BT can accommodate all probability values. In terms of calculating the final probability of H, Pr(H | E & B), we use the same formula–BT–regardless of whether H is an extraordinary claim. From a mathematical perspective, it makes no difference whatsoever whether we label a claim “extraordinary” or “ordinary.” We can use BT to assess the epistemic probabilities of both types of claims.