If you read this blog, chances are that you very familiar with the slogan, popularized by the late Carl Sagan, that “Extraordinary claims require extraordinary evidence.” What I want to do is to offer a Bayesian interpretation and defense of that slogan. In order to make this a ‘self-contained’ post, I will need to repeat some of what I’ve written elsewhere. Epistemic Probability

In this article, when I refer to probability I shall be adopting the epistemic interpretation of probability. The epistemic probability of a statement is a measure of the probability that a statement is true, given some stock of knowledge. In other words, epistemic probability measures a person’s degree of belief in a statement, given some body of evidence. The epistemic probability of a statement can vary from person to person and from time to time (based upon what knowledge a given person had at a given time).[1] For example, the epistemic personal probability that a factory worker Joe will get a pay raise might be different for Joe than it is for Joe’s supervisor, due to differences in their knowledge.

Two Types of Evidence and Corresponding Probabilities

Let us divide the evidence relevant to naturalism and theism into two categories. First, certain items of evidence function as “odd” facts that need to be explained. Second, other items of evidence are background evidence, which determine the prior probability of rival theories and partially determine their explanatory power.

These two types of evidence have two probabilistic counterparts which are useful for evaluating explanatory hypotheses: (1) the prior probability and (2) the explanatory power of a hypothesis H. (1) is a measure of how likely H is to occur based on background information B alone, whether or not E is true. As for (2), this measures the ability of a hypothesis (combined with background evidence B) to predict (i.e., make probable) an item of evidence. [2]

Notation

Let us proceed, then, to defining some basic probabilistic notation.

B: background evidence

E: the evidence to be explained

H: an explanatory hypothesis

Ri: the rival explanatory hypotheses to H

Pr(x): the probability of x

Pr(x | y): the probability of x conditional upon y

Next, let us define the following conditional probabilities.

Pr(H | B) = the prior probability of H with respect to B—a measure of how likely His to occur at all, whether or not E is true.

Pr(Ri | B) = the prior probability of Riwith respect to B—a measure of how likely Ri is to occur at all, whether or not E is true.

Pr(E | H & B) = the explanatory power of H—a measure of the degree to which the hypothesis Hpredicts the data E given B.

Pr(E | Ri & B) = the explanatory power of Ri—a measure of the degree to which Ri predicts E given B.

Pr(H | E& B) = the final probability that His true conditional upon the total evidence Band E.

The Probabilistic Interpretation of “Extraordinary Claims” Using this notation, it is possible to provide a mathematically rigorous definition of an extraordinary claim. An extraordinary claim may be defined as an explanatory hypothesis which is extremely improbable, conditional upon background information alone, i.e., Pr(H | B) <<< 0.5. Because we are using the epistemic interpretation of probability, it follows that what counts as an “extraordinary claim
” may vary from person to person and from time to time. For example, a healing miracle attributed to the Virgin Mary will be a very extraordinary claim to naturalists (and perhaps? non-Catholics), but not as extraordinary (or not extraordinary at all) to Catholics. With “extraordinary claim” defined, let us now define what constitutes extraordinary evidence. Before we do, however, we must first review Bayes’s Theorem. Bayes’s Theorem

Bayes’s Theorem is a mathematical formula which can be used to represent the effect of new information upon our degree of belief in a hypothesis. In its general form, Bayes’s Theorem may be expressed as follows:

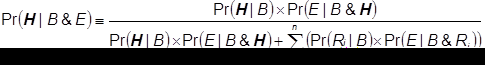
With Bayes’s Theorem defined, we are now in a position to offer a mathematically rigorous definition of “extraordinary evidence.”

The Bayesian Interpretation of “Extraordinary Evidence”

It follows from Bayes’s Theorem that H will have a high final epistemic probability on the evidence B and E:

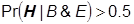
just in case it has a greater overall balance of prior probability and explanatory power than do its alternatives collectively:

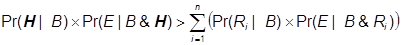
Thus, “extraordinary evidence” can be interpreted as the requirement that a hypothesis’s explanatory power is proportionally high enough to offset its prior improbability (the “extraordinary claim”). Proposal for Both Theists and Naturalists Regarding Extraordinary Claims Because background information plays such a crucial role in determining the prior probability of any hypothesis, extraordinary or not, one thing that both theists and naturalists could do to improve communication with one another is to explicitly identify the propositions which make up their background information. Doing so will not magically resolve their disagreements, but it will greatly improve the chances that the two parties are at least understanding one another. For an example of what this might look like, see any of the individual arguments for naturalism in my series on evidential arguments for naturalism.

Notes [1] Brian Skyrms, Choice & Chance: An Introduction to Inductive Logic (4th ed., Belmont: Wadsworth, 2000), 23. [2] I owe these definitions to Robert Greg Cavin in private correspondence.