Geisler & Turek Rebuttal: Chapter 9 (Part 2)
Chapter 9. Do We Have Early Eyewitness Testimony about Jesus?
By Matthew Wade Ferguson and Jeffery Jay Lowder
(This post continues where part 1 left off.)
(ii) New Testament Textual Accuracy: “Textual accuracy” measures the degree to which copies of a document match that of the original document. Although none of the original New Testament documents have survived, Geisler and Turek argue that the textual accuracy of the New Testament documents is superior to that of other ancient documents. In their words:
In fact, the New Testament documents have more manuscripts, earlier manuscripts, and more abundantly supported manuscripts than the best ten pieces of classical literature combined. (225)
We agree with Geisler and Turek. If someone were to fallaciously claim that the New Testament can’t be trusted, as a whole, because it has been textually corrupted, then Geisler and Turek would be correct to object that this is false, because we have (mostly) reliable manuscripts.
By the same token, however, the New Testament’s textual accuracy does not improve its historical accuracy. Accurate textual transmission can preserve the historical accuracy of a work that was originally historically reliable, but it can do nothing to improve or save the historical accuracy of a work that was originally based on ahistorical legends. With that in mind, let us turn now to the question of historical accuracy.
(iii) New Testament Historical Accuracy: In this section, Geisler and Turek attempt to do three things: (a) propose seven historical criteria or tests to “determine whether or not to believe a given historical document” (230); (b) refute common objections to the reliability of the New Testament; and (c) argue that the NT documents are early.
Regarding (a) the historical tests, Geisler and Turek list the following seven tests: (1) do we have early testimony; (2) eyewitness testimony; (3) multiple, independent eyewitness sources; (4) trustworthiness; (5) corroborating evidence from archaeology or other writers; (6) enemy attestation; and (7) embarrassing details. According to them, “documents that meet most or all of these historical tests are considered trustworthy beyond a reasonable doubt” (231).
Let’s “zoom out” for a moment from the topic of the NT’s historical reliability and instead look at how this argument fits into Geisler’s and Turek’s “Twelve Points that Show Christianity Is True.” Geisler and Turek seek to defend the following inference:
6. The New Testament is historically reliable.
7. The New Testament says Jesus claimed to be God.
8. Jesus’ claim to be God was miraculously confirmed by
a. His fulfillment of many prophecies about himself;
b. His sinless life and miraculous deeds;
c. His prediction and accomplishment of his resurrection. (28)
Geisler’s and Turek’s statement about historical tests, as well as points 6-8 of their twelve-point case for Christianity, suggests a previously unnamed version of an existing inductive argument form, which we shall call the “argument from general reliability.” Before we can introduce that argument form, however, we first need to review its “parent” argument known, the statistical syllogism. Statistical syllogisms have the following logical structure or form.
(1) Z percent of F are G.
(2) x is F.
(3) [Z% probable] Therefore, x is G.
One “child” version of the statistical syllogism is the argument from authority, which we discussed in chapter six. The simple version of the argument from general reliability is another “child” version of the statistical syllogism. It has the following structure.
(4) Source S is generally reliable.
(5) S reports that event E occurred.
(6) [probable] E occurred.
With this schema in place, let’s return to Geisler’s and Turek’s statement, “documents that meet most or all of these historical tests are considered trustworthy beyond a reasonable doubt.” If we replace S with “The New Testament documents” and E with “E1, …, En” (to represent the events reported by the New Testament documents), then Geisler’s and Turek’s simple argument from general historical reliability may be summarized as follows.
(4’) The New Testament documents are generally historically reliable.
(5’) The New Testament documents report that E1, …, En occurred.
(6’) [probable] E1, …, En occurred.
What Geisler and Turek fail to realize, however, is that general historical reliability alone does not suffice to make it probable, much less probable “beyond a reasonable doubt,” that event E1, …, En occurred. Although simple arguments from reliability are statistical syllogisms, simple arguments from reliability are logically incorrect because they violate the inductive Total Evidence Requirement. Such arguments ignore information about the base rates of events like E1, …, En and instead consider only information about the reliability of the historical source which reports E1, …, En. Statisticians call this error the base rate fallacy.
In order to fully appreciate the force of this objection, let’s turn to a non-theological example, one which is actually quite famous in the academic literature about reasoning under uncertainty. Amos Tversky and Daniel Kahnemann, the authors of this example, describe it as follows.[1]
A cab was involved in a hit-and-run accident at night. Two cab companies, the Green and the Blue, operate in the city. You are given the following data:
(a) 85% of the cabs in the city are Green and 15% are Blue.
(b) A witness identified the cab as Blue. The court tested the reliability of the witness under the same circumstances that existed on the night of the accident and concluded that the witness correctly identified each one of the two colors 80% of the time and failed 20% of the time.
What is the probability that the cab involved in the accident was Blue rather than Green?
If you answered “There is an 80% probability the cab was blue,” you are in good company. Most people who consider this example say that the answer is “blue” because they are impressed by the witness’s 80% reliability. They seem to be implicitly appealing to the following simple version of the argument from general reliability.
(7) 80% of cab identifications made by witness W under conditions similar to those at the time of the hit-and-run accident are correct.
(8) W’s identification of the cab involved in the hit-and-run accident as a blue cab is a cab identification made by W under similar conditions.
(9) [80% probable] W’s identification of the cab involved in the hit-and-run accident as a blue cab is correct, i.e., a blue cab was involved in the hit-and-run accident.
The correct answer, however, is “There is a 59% probability the cab was green.” The argument in (7)-(9) is logically incorrect because its reference class (“cab identifications made by witness W under conditions similar to those at the time of the hit-and-run accident”) violates the requirement of total evidence. It does this by ignoring what we know about the base rates of green and blue cabs, i.e., the proportion of cabs that are green (85%) is much greater than the proportion of cabs that are blue (15%). Therefore, despite W’s 80% reliability, the most likely explanation (probability=59%) is that W is mistaken and he actually saw a green cab.
Still not convinced? Imagine that the town has exactly 1,000 cabs, so that 85%=850 and 15%=150. Then the breakdown in cabs can be shown by the diagram in Figure 2.
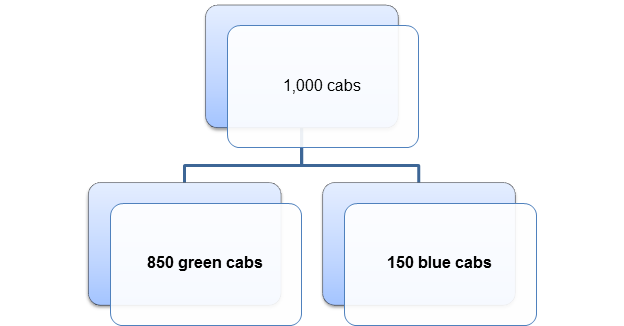
Figure 2
Since W is 80% accurate, when he testifies about the 850 green cabs, he will correctly testify that 80% of those 850 cabs (=680) were green and he will incorrectly testify that 20% of those 850 cabs (=170) were blue. This is shown below in Figure 3.
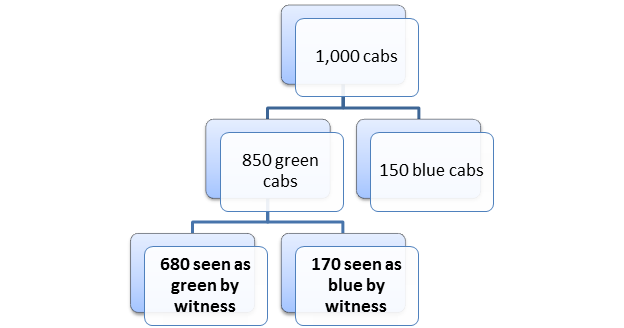
Figure 3
Similarly, when W testifies about the 150 blue cabs, he will correctly testify that 80% of those 150 blue cabs (=120) were blue and he will incorrectly testify that 20% of those 150 blue cabs (=30) were green. This is shown in Figure 4.
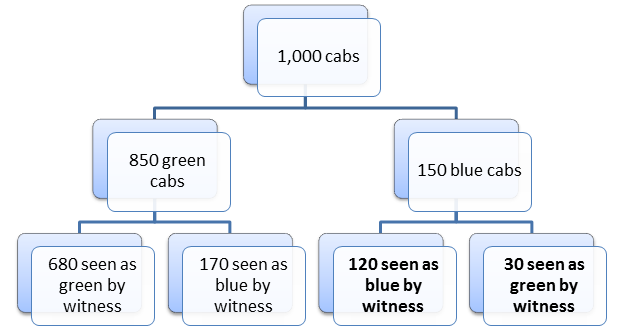
Figure 4
Let’s now return to our question: if an 80% reliable witness testifies the cab was blue, is it more likely that the cab was blue or green? The diagram in Figure 4 makes it easy to correctly calculate the probability, without having to remember the probability theorem known as Bayes’s Theorem. If we want to calculate the probability that the cab was blue, we take the number of times W correctly testified that the cab was blue (120) and divide it by the total number of times W testified that the cab was blue (170+120=290). In probability notation:
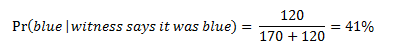
Similarly, if we want to calculate the probability that the cab was green, we take the number of times W incorrectly testified that the cab was blue (170) and divide it by the total number of times W testified that the cab was blue (170+120=290). In probability notation:
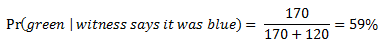
Although an 80% reliable witness testified the cab was blue, it is more likely that the cab was green because there are so many more green cabs than blue cabs. Our specific information about W’s reliability has been outweighed by our general information about the base rates of green and blue cabs. In the words of Tversky and Kahnemann, “In spite of the witness’s report, therefore, the hit-and-run cab is more likely to be Green than Blue, because the base rate is more extreme than the witness is credible.”[2]
Thus, instead of the statistical syllogism in (7)-(9), we should instead use a modified version, which we may call the complex version of the argument from general reliability.
(7’) 59% of all blue cab identifications made by W under similar conditions are incorrect.
(8’) W’s identification of the cab involved in the hit-and-run accident as a blue cab is a blue cab identification made by W under similar conditions.
(10) The percentage stated in (7’) correctly incorporates the available information about the base rates of blue cabs.
(9’) [59% probable] W’s identification of the cab involved in the hit-and-run accident as a blue cab is incorrect.
We have shown that simple versions of arguments from reliability to the historicity of an event are logically incorrect by ignoring information about the base rate of events of that type and, consequently, by using a reference class which fails to embody the total available evidence.
This, in turn, entails that Geisler’s and Turek’s twelve-point case for Christianity is, at best, incomplete. In order to show that the New Testament’s historical claims—such as the claim that Jesus was crucified, died, was buried, and so forth—are probably true, Geisler and Turek must do more than defend the general historical reliability of the New Testament. They must also show that this general historical reliability is not outweighed by the base rates of those events.
Notes
[1] Amos Tversky and Daniel Kahnemann, “Evidential Impact of Base Rates,” Judgment under Uncertainty: Heurists and Biases (ed. Daniel Kahnemann, Paul Slovic, and Amos Tversky, New York: Cambridge University Press, 1982), 156-57.
[2] Tversky and Kahnemann 1982, 157.



