Extraordinary Claims Require Extraordinary Evidence (ECREE), Part 4: NT Reliability, Extraordinary Claims, and the Base Rate Fallacy

|

I want to re-visit the issue of “extraordinary claims require extraordinary evidence” (ECREE), by considering a type or class of argument for miracles based upon the historical reliability of the New Testament (NT), hereafter “the argument.” According to this argument, the general historical reliability of the NT provides sufficient evidence to make the historicity of NT miracles more probable than not. I shall argue, however, that this argument commits the base rate fallacy and therefore is inductively incorrect. While the base rate fallacy is not a new idea, its possible application to the argument is, so far as I can tell, a neglected topic in discussions about NT miracles.

The Argument Formulated

I shall formulate the argument from NT reliability to the historicity of NT miracles as an explanatory argument.

B: The Relevant Background Evidence

B1. The New Testament is generally historically reliable.

E: The Evidence to be Explained

E1. The New Testament text reports that some miracle, M, occurred.

H: The Proposed Explanatory Hypothesis and Its Alternatives

H: The reported miracle, M, actually happened.
~H: M did not happen.

Argument

(1) E is known to be true, i.e., Pr(E | B) is close to 1.
(2) E is antecedently more probable on H than on ~H, i.e., Pr(E | H & B) > Pr(E | ~H & B).
(3) Therefore, other evidence held equal, H is probably true, i.e., Pr(H | B & E) > 0.5.

The Base Rate Fallacy

A police officer testifies she saw a blue cab. The police officer gets the color of the cab right 95% of the time she testifies. In her area, 99% of the taxis are green cabs and 1% of the taxis are blue. What is the most probable color of the cab seen by the police officer?

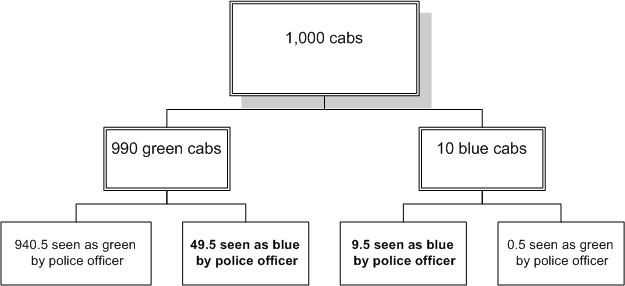
The correct answer is green. The base rate of green cabs is much higher than that of blue cabs, i.e., the proportion of cabs that are green (99%) is much greater than the proportion of cabs that are blue (1%). Therefore, despite the witness’s 95% reliability, the most likely explanation is that the police officer is mistaken and she actually saw a green cab. 
 
To make things easy, assume the town has exactly 1,000 cabs. The following diagram then shows why the correct answer is green.
 


Let Pr(Green | testimony that it was blue) be the probability that the cab was green conditional upon the police officer’s testimony that it was blue.

Pr(Green | testimony that it was blue) = 49.5 / (49.5 + 9.5) = 49.5 / 59 = 83.9%.

People who answer “blue” have unwittingly committed the base rate fallacy: they have ignored the information about the base rates of green and blue cabs and considered only the information about the reliability of the witness.

Let us now turn to the argument from NT reliability to the historicity of NT miracles.

The Argument Evaluated

Comments on B1

Again, B1 is the statement, “The New Testament is generally historically reliable.” By “generally historically reliable,” I mean simply that its empirical claims–i.e., statements about events which allegedly occurred in the past–are often true.

Comments on (3)

The fatal flaw with this argument is its premise (3). Just as in the police officer example above, the argument commits the base rate fallacy. It focuses solely on the general historical reliability of the NT and says nothing about the base rate of the purported miracle in question. Therefore, the argument is inductively incorrect: it fails to establish a high epistemic probability for its conclusion.