The question “Who moved the stone?” is used by Christian apologists to raise an objection against some skeptical theories about the alleged resurrection of Jesus, especially the Swoon Theory (see Objection #7 in Handbook of Christian Apologetics by Peter Kreeft and Ronald Tacelli, p.183-184), but also the Conspiracy Theory, and the Hallucination Theory.

In Part 1 of this series, I argued on the basis of examples that one normal healthy adult could easily move even a larger-sized circular stone, even if that stone weighed 2,300 pounds. For example, in 2009 Kevin Fast pulled a 208-ton airplane for 28 feet in less than two minutes (because the airplane was on wheels).

In Part 2 of this series, I argued on the basis of calculations of the force required to overcome rolling resistance that one healthy non-disabled adult could easily move a circular blocking stone that is the size and weight of the blocking stone used at the tomb of Jesus (assuming a circular blocking stone was used), contrary to the claims of many Christian apologists.

Most stone tombs in and around Jerusalem in the 2nd Temple period (which includes the years Jesus was around) had, however, square blocking stones. Only a few circular blocking stones have been discovered from that time and location, and they were for tombs of very wealthy and powerful families. On the other hand, numerous square blocking stones have been discovered in and near Jerusalem for tombs from the 2nd Temple period. So, archeology casts some doubt on the view that a circular blocking stone was used at the tomb of Jesus (see “How Was Jesus’ Tomb Sealed?” on the Biblical Archaeology Society website).

Obviously, a square blocking stone cannot be easily rolled the way that a circular blocking stone could be rolled. It would clearly be more difficult to move a square-blocking stone than to move a circular-blocking stone. However, it is not immediately obvious whether one healthy adult who was not disabled could move a square-blocking stone from the entrance to a stone tomb.

In Part 3 of this series, I estimated the volume of a smaller square blocking stone (one that would be large enough to close off a smaller-sized entrance to a stone tomb) to be about 6.44 cubic feet, and that, depending on the kind of stone it was made from, it would probably weigh between 960 and 1,170 pounds.

If such a smaller square blocking stone was composed of limestone, it would weigh about 966 pounds. Could just ONE non-handicapped adult of normal strength move such a square blocking stone away from the entrance of a stone tomb?

Such a stone would be too heavy for an adult of normal strength to lift up off the ground. The average man without any special training can deadlift about 155 pounds, and with a couple of months of practice can deadlift about 285 pounds. (see “How Much Can the Average Man Lift?”). The current world record for deadlifting is 1,104.5 pounds (see “Progression of the deadlift world record”). So, an adult of normal strength would not be able to lift up a 966-pound stone up off the ground. Furthermore, since the top of the “cork” section of a square blocking stone would be up against the top of the entrance to the tomb (when the stone is in place to close off the tomb), there is no room for a square blocking stone to move upwards until the stone has been pulled (or pushed) out of the entrance.

Pushing or pulling a square blocking stone away from the entrance of a stone tomb would usually involve dragging the stone on a stone surface in front of the tomb. The amount of friction that needs to be overcome depends partly on the weight of the blocking stone and partly on the type of stone it is made from, and partly on the type of stone surface it is dragged over.

BLOCKING STONE MADE OF LIMESTONE & SURFACE MADE OF LIMESTONE

A blocking stone made out of limestone would create a great deal of friction if dragged over a surface that was also limestone. The coefficient of friction for a limestone object dragged over a limestone surface is .75:

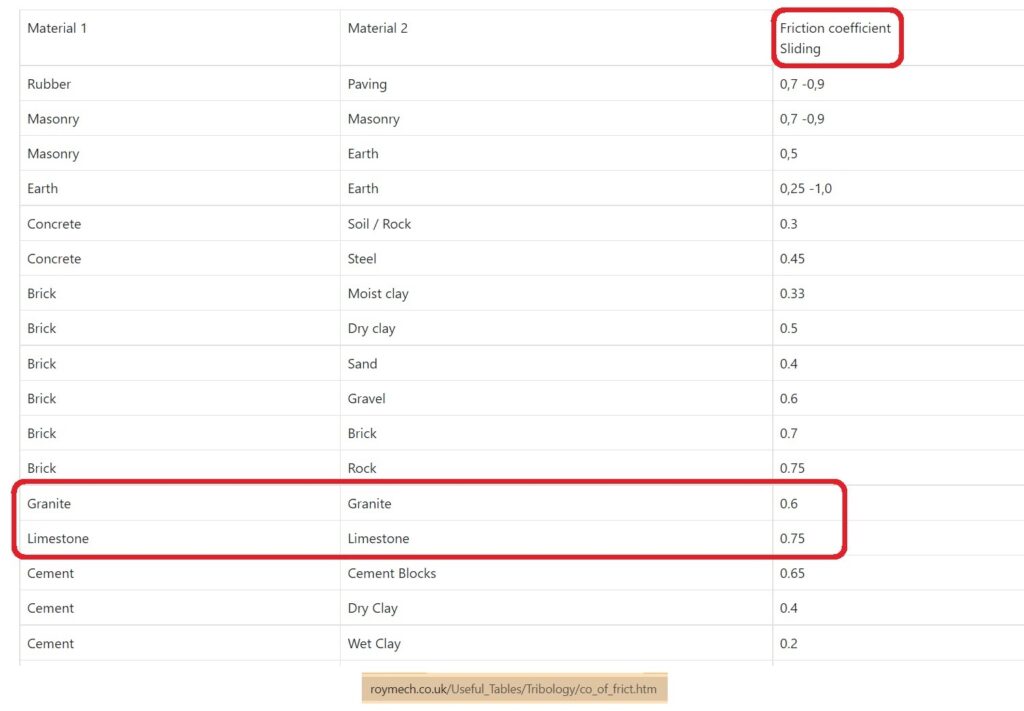
That means that dragging a square blocking stone made from limestone over a surface consisting of limestone requires a force that is 75% of the weight of the blocking stone:

966 pounds x .75 = 724.5 pounds of force

That is too much force for an adult of average strength to generate by pushing or pulling. For example, I can barely do just one pullup. That means that if I try really hard, I can barely lift my own weight off the ground. I weigh 220 pounds, so 220 pounds is the most force I can generate by pulling with my arms. So, clearly, I could not pull with 724.5 pounds of force, using my arms.

However, it is not necessary to drag the whole square blocking stone all at once. It would require much less force to pull out the left side of the blocking stone a few inches, then pull out the right side of the blocking stone a few inches, and go back and forth pulling one side out a few inches at a time. In fact, it would require only HALF the force to move the stone in this manner.

I experimented with dragging a rectangular brick-sized stone across the concrete surface of my carport. When I dragged the whole stone at a slow and steady pace, that required 9.0 pounds of force (measured with a spring scale used to weigh fish). But when I just dragged one end of the stone, pivoting the stone like a door on a hinge, allowing the other end of the stone to stay in place, I was able to drag the one end with only 4.5 pounds of force, or HALF the force required to drag the whole stone.

We have calculated that 724.5 pounds of force would be required to drag the whole square blocking stone across a limestone surface. But if instead of dragging the whole stone all at once, we pull (or push) out the left side of the stone a few inches, and then pull (or push) the right side of the stone out a few inches, and go back-and-forth that way until the blocking stone was out of the entrance, this would require only about HALF that force:

724.5 pounds of force / 2 = 362.25 pounds of force

USING ONE’S LEGS INSTEAD OF ONE’S ARMS

I can pull with about 220 pounds of force for a few seconds. That would not be enough to move this smaller blocking stone, even if I tried to pull it outward just a few inches on one side.

However, a person’s legs are stronger than a person’s arms, in most cases. Although I can only pull with about 220 pounds of force with my arms, I can push with about 380 pounds of force with my legs. If I put my bathroom scale up against a wall, sit on the floor with my legs partially bent and my feet on the scale, I can push against the scale so that the scale reads over 380 pounds, at least for a few seconds, if my back is up against a solid surface.

So, if I was inside of a stone tomb, sitting on the floor of the tomb with my legs partially bent and my feet placed up against the right side of the interior surface of the “cork” of a square blocking stone, and my back was up against something solid (a large stone or a stone bench or a stone wall), then I could put 380 pounds of force on the right side of the interior surface of the square blocking stone and move that side of that stone a few inches outwards. I could then move my feet to the left side of the interior surface of the “cork” of the blocking stone and push it a few inches outwards. I could alternate back and forth between the right and left sides of the blocking stone and push the stone a foot or more outwards. Thus, there is enough strength in the pushing force that I can generate with my legs to push a smaller-sized square blocking stone away from the entrance of a stone tomb, from inside the tomb.

I am not a weight lifter, nor do I work out at a gym. My legs are in OK shape because I walk a mile or two most days, but that is about the only exercise my legs get. Thus, there is good reason to believe that most normal adults who are not handicapped could generate 362 pounds of force with their legs, and thus move a smaller-sized blocking stone from the entrance of a stone tomb, from the inside of the tomb.

MOVING THE STONE FROM OUTSIDE THE TOMB

But what about from the outside of the tomb? Although I can only produce about 220 pounds of pulling force with my arms, that is for a steady pull.

If a door with a large handle was stuck closed, and if there was a large fire inside the building and I wanted to get into the building to rescue someone, I would first try a steady pull on the door handle. But if the door did not budge, then I would try to pull on the handle with a sudden jerking force, throwing my body backward while tightly gripping the handle with both hands. The motion of my body moving rapidly away from the door would add to the pulling force exerted by the muscles in my arms, and this would allow me to generate significantly more pulling force than with just a steady pull on the handle.

In northern Spain, there are contests of strength where people drag large and heavy stones as far as they can in a designated amount of time (e.g. in 20 minutes). The stones dragged by a single person can weigh between 700 and 800 kilograms (1,543 pounds to 1,764 pounds). The athletes who compete in these contests lurch backward and pull on a handle attached to a chain wrapped around the stone. This quick but forceful pull on the handle moves the heavy stone a few inches (like 3 to 6 inches):

If one could get a sturdy wood pole or staff behind the edge of the “lid” of a square blocking stone and lurch backward away from the entrance, holding onto the right and left portions of the pole or staff and pulling the pole or staff quickly, one could generate significantly more than just 220 pounds of pulling force, at least for a second or two, and that might well be sufficient to move one side of a square blocking stone outwards a few inches.

Another possibility is the use of a board as a lever. This would only require a fairly short board, say two or three feet long. One end of the board could be wedged under the left-hand edge of the “lid” of the blocking stone, a fulcrum point (consisting of a stone or small piece of wood) could be placed a foot or so to the left of where the board is wedged under the edge of the “lid”, and a person could use their legs and feet to push on the end of the board that is one or two feet to the left of the fulcrum point. If the fulcrum point was halfway along the length of the board, then about 362 pounds of force would need to be applied to the end of the board to the left of the fulcrum point in order to exert 362 pounds of force on the back of the left-hand edge of the “lid”, thus moving the left side of the blocking stone a few inches outwards.

Since I can generate at least 380 pounds of pushing force with my legs, there is good reason to think that most normal adults without a handicap could generate 362 pounds of pushing force with their legs. Thus, with the use of a short board, most normal adults could use their legs to move a smaller-sized square blocking stone a few inches outwards from the entrance of the tomb. And then they could alternate between the left and right sides of the blocking stone, moving the stone a few inches further with each effort, until the blocking stone was moved a foot or so outwards from the entrance.

If the fulcrum point was placed one-third of the length of the board from the entrance (e.g. fulcrum point for a three-foot-long board placed one foot away from the edge of the “lid” of the blocking stone, leaving two feet of the board on the other side of the fulcrum point to push on), that would DOUBLE the force applied by the use of a person’s legs. Thus, only 185 pounds of force on the far end of the board would create 370 pounds of force on the other end of the board to push the “lid” of the blocking stone away from the entrance of the tomb. Even a smaller or weaker adult would likely be able to generate 185 pounds of force with his or her legs, and thus would be able to move one side of the blocking stone at least a few inches away from the entrance to the tomb.

BLOCKING STONE MADE OF LOW-DENSITY GRANITE

What if the blocking stone was made of granite instead of limestone? What if the stone surface under the blocking stone was also granite? How much force would be needed to move such a stone on such a surface? The volume of a smaller square blocking stone would be about 6.44 cubic feet. If such a blocking stone was composed of low-density granite, it would weigh about 1,024 pounds (see Part 3 of this series). A granite stone weighs more than one composed of limestone. However, the coefficient of friction for dragging a granite stone across a granite surface is .6, which is a bit lower than the coefficient of friction for dragging a limestone stone across a limestone surface.

The force required to move this low-density granite blocking stone across a granite surface is this:

1,024 pounds x .6 = 614.4 pounds of force

But only HALF of that force would be required to move just one side of the blocking stone at a time:

614.4 pounds of force / 2 = 307.2 pounds of force

So, although a blocking stone composed of granite weighs significantly MORE than a blocking stone composed of limestone, it would actually require significantly LESS force to be moved than a blocking stone composed of limestone, at least if the surface it was resting on was also composed of granite.

What if the blocking stone was composed of granite, but the surface it rested upon was composed of limestone? In that case the coefficient of friction would be LESS than limestone-on-limestone but MORE than granite-on-granite. The coefficient of friction for granite on limestone would probably be about the average between those two scenarios:

(.75 + .6 )/ 2 = 1.35 / 2 = .675

Thus, the coefficient of friction for a blocking stone composed of granite being dragged across a surface composed of limestone would be about: .68.

1,024 pounds x .68 = 696.3 pounds of force

Only HALF of that force would be required to move just one side of the blocking stone at a time:

696.3 pounds of force / 2 = 348.2 pounds of force

This is still LESS force than what would be required to move a small square blocking stone composed of limestone across a limestone surface. Therefore, because it appears to be possible for just ONE normal non-handicapped adult to move a small square blocking stone composed of limestone away from the entrance of the tomb, assuming it rested on a limestone surface, it would also be possible for just ONE normal non-handicapped adult to move a small square blocking stone composed of low-density granite away from the entrance of the tomb, if the surface it rests upon was either composed of granite or composed of limestone.

BLOCKING STONE MADE OF HIGH-DENSITY GRANITE

The volume of a smaller square blocking stone would be about 6.44 cubic feet. If such a blocking stone was composed of high-density granite, it would weigh about 1,159 pounds (see Part 3 of this series). A granite stone weighs more than one composed of limestone. However, the coefficient of friction for dragging a granite stone across a granite surface is .6, which is a bit lower than the coefficient of friction for dragging a limestone stone across a limestone surface.

The force required to move this high-density granite blocking stone across a granite surface is this:

1,159 pounds x .6 = 695.4 pounds of force

But only HALF of that force would be required to move just one side of the blocking stone at a time:

695.4 pounds of force / 2 = 347.7 pounds of force

So, although a blocking stone composed of high-density granite weighs significantly MORE than a blocking stone composed of limestone, it would actually require LESS force to be moved than a blocking stone composed of limestone, at least if the surface that the high-density granite blocking stone was resting on was also composed of granite. Thus, just ONE normal non-handicapped adult could move such a blocking stone from the entrance to the tomb, if the surface the blocking stone rested upon was composed of granite.

How much force is required to move such a blocking stone on a surface composed of limestone? As we noted above, the coefficient of friction would be about .68 for dragging a granite blocking stone over a limestone surface:

1,159 pounds x .68 = 788.1 pounds of force

Only HALF that force would be required to move just one side of the blocking stone at a time:

788.1 pounds of force / 2 = 394.1 pounds of force

I might be able to produce 394.1 pounds of force with my legs if I tried really hard, but that amount of force might be a little too much for my legs to produce. I’m sure that some normal adults can produce that much force with their legs, but I don’t know if 10% of normal adults could do this, or 30%, or 60%, or 80%.

With a three-foot board and a fulcrum point placed one foot away from the left edge of the blocking stone, I could easily apply 198 pounds of force on the left end of the board using my legs and feet, and this would produce 396 pounds of force on the back of the lid of the blocking stone, which would be enough to move that stone a few inches out of the entrance to the tomb. So, with the help of a short board, I could move this smaller-sized square blocking stone composed of high-density granite away from the entrance of the tomb, even if the surface the blocking stone was resting upon was composed of limestone. Thus, it is possible for just ONE normal non-handicapped adult to move such a blocking stone away from the entrance of the tomb, even if the surface the blocking stone was resting upon was composed of limestone.

CONCLUSION

I have examined the force required to move a smaller-sized square blocking stone, given various combinations of materials:

• limestone blocking stone on a surface of limestone
• low-density granite blocking stone on a surface of granite
• low-density granite blocking stone on a surface of limestone
• high-density granite blocking stone on a surface of granite
• high-density granite blocking stone on a surface of limestone

In each case, it appears to be possible for just ONE normal non-handicapped adult to move the square blocking stone away from the entrance of the tomb.

Since we do not know whether the size of the entrance to the tomb of Jesus was smaller (2.0 feet wide x 2.5 feet tall) or larger (2.5 feet wide x 3.0 feet tall), or somewhere in between those dimensions, it might well have been a smaller-sized entrance, and in that case, a smaller-sized square blocking stone that would fit in such an entrance could be moved from the entrance by just ONE normal non-handicapped adult. Therefore, Christian Apologists cannot rule out the scenario in which just ONE adult was able to move a square blocking stone from the entrance to Jesus’ tomb.