The question “Who moved the stone?” is used by Christian apologists to raise an objection against some skeptical theories about the alleged resurrection of Jesus, especially the Swoon Theory (see Objection #7 in Handbook of Christian Apologetics by Peter Kreeft and Ronald Tacelli, p.183-184), but also the Conspiracy Theory, and the Hallucination Theory.

In Part 1 of this series, I argued that a circular blocking stone large enough to block a smaller-sized entrance to a tomb (2.0 feet x 2.5 feet) would be 3.2 feet in diameter and about ten inches thick, and have a volume of 6.7 cubic feet and that such a smaller circular stone would weigh at least 1,005 pounds.

I also argued that a circular blocking stone large enough to block a larger-sized entrance to a tomb (2.5 feet x 3.0 feet) would be 3.9 feet in diameter and 12 inches thick. I rounded the diameter to 4.0 feet and calculated the volume of such a larger stone to be 12.57 cubic feet. Such a larger circular stone would weigh between 1,886 pounds and 2,263 pounds, depending on the type of stone from which it was made. I concluded that if a circular stone was used to block Jesus’ tomb, the stone probably weighed between 1,000 pounds and 2,300 pounds.

In Part 1 of this series, I also argued on the basis of examples that one normal healthy adult could easily move even the larger-sized circular stone, even if that stone weighed 2,300 pounds. For example, in 2009 Kevin Fast pulled a 208-ton airplane for 28 feet in less than two minutes (because the airplane was on wheels).

In Part 2 of this series, I argued on the basis of calculations of the force required to overcome rolling resistance that one healthy non-disabled adult could easily move a circular blocking stone that is the size and weight of the blocking stone used at the tomb of Jesus (assuming a circular blocking stone was used), contrary to the claims of many Christian apologists.

Most stone tombs in and around Jerusalem in the 2nd Temple period (which includes the years Jesus was around) had square blocking stones. Only a few circular blocking stones have been discovered from that time and location, and they were for tombs of very wealthy and powerful families. However, numerous square blocking stones have been discovered in and near Jerusalem for tombs from the 2nd Temple period. So, archeology casts some doubt on the view that a circular blocking stone was used at the tomb of Jesus.

Obviously, a square blocking stone cannot be easily rolled the way that a circular blocking stone could be rolled. It would clearly be more difficult to move a square-blocking stone than to move a circular-blocking stone. However, it is not immediately obvious whether one healthy adult who was not disabled could move a square-blocking stone from the entrance to a stone tomb.

THE SHAPE OF A SQUARE BLOCKING STONE

Square blocking stones were a bit like cork bottle stoppers. The end that was pushed into the entrance was smaller and narrower than the other end, so that the stone could fit tightly and “seal” the entrance off, like a cork fitting into the neck of a bottle:

But square blocking stones generally also had a “lid” that stayed on the outside of the entrance, like some bottle stoppers have:

So, a square blocking stone usually had two parts: the part that pushed into the tomb (call it the “cork”), and the part that remained outside the tomb (call it the “lid”). Here are a couple examples of square blocking stones:

DIMENSIONS OF A SMALLER SQUARE BLOCKING STONE

Because the dimensions of a smaller entrance to a stone tomb in the 2nd Temple period were about 2.0 feet wide by 2.5 feet tall, we can estimate the dimensions of a square blocking stone that would be large enough to close off an entrance of that smaller size.

The size of the “lid” on such a square blocking stone would be a bit larger than the size of the entrance. A reasonable estimate of the “lid” dimensions would be four to six inches wider on each side of the entrance and four to six inches taller than the entrance. Since I will later estimate the dimensions of a square blocking stone for a larger tomb entrance, I will use the four inches estimate for this smaller stone, and the six inches estimate for the larger stone. A reasonable estimate for the thickness of the lid would also be four to six inches. So, I will again use the smaller estimate of four inches thick for the smaller stone lid and six inches for the thickness of the larger stone lid.

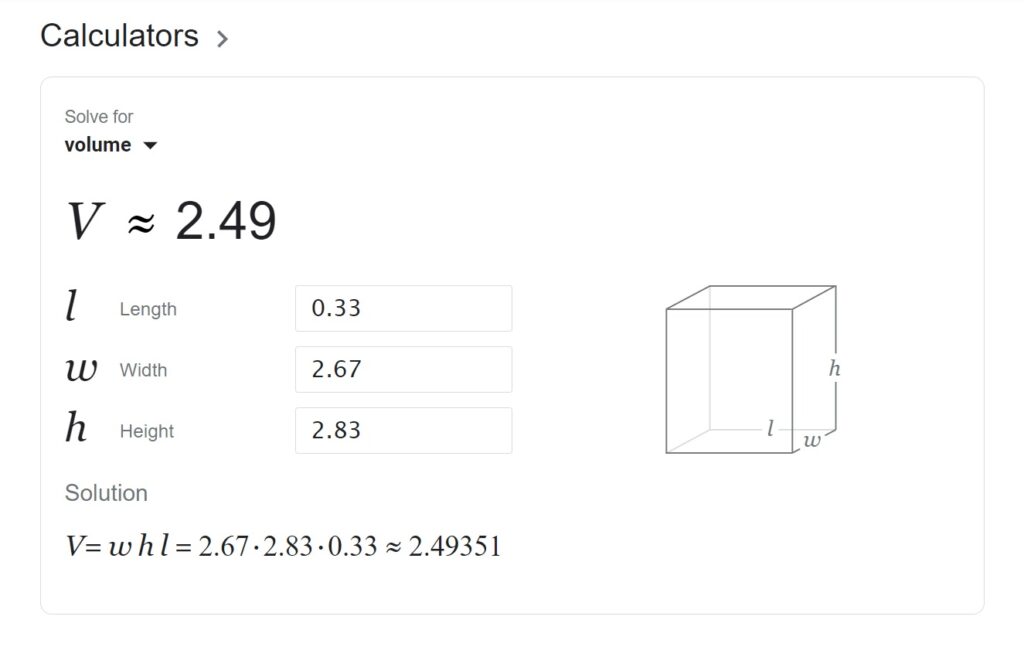
This gives us estimated dimensions for the lid of a square blocking stone that would cover a smaller-sized entrance to a stone tomb. With four inches added to the left side and four inches added to the right side, the lid would be a total of eight inches wider than the entrance: 2 feet 8 inches wide (2.67 feet wide). With four inches added to the height of the entrance, the lid would be four inches taller than the entrance: 2.5 feet plus 4 inches = 2 feet 10 inches tall (2.83 feet tall). The lid of this smaller square blocking stone would be about 4 inches thick (0.33 feet thick). Therefore, the estimated volume of the lid of a smaller quare blocking stone would be: 2.67 feet x 2.83 feet x 0.33 feet = 2.49 cubic feet.

The “cork” part of the blocking stone protrudes into the tomb a ways to act like a stopper in the neck of a bottle (and also to give the stone some heft, so that the stone cannot be easily knocked over and away from the entrance). How far into the tomb would the cork extend? A reasonable estimate is that it would extend between one foot and a foot and a half into the tomb. Because I will later estimate the dimensions of a square blocking stone for a larger sized entrance, I will use the smaller size of one foot for the size of this smaller square blocking stone, and will use one and a half feet for the size of the larger square blocking stone later.

The “cork” part of the blocking stone would be smaller at the end that goes into the tomb as compared to the size of the “cork” where it joins the “lid”. A reasonable estimate is that the end that goes into the tomb would be four to six inches narrower on each side, and four to six inches shorter than the height of the entrance. The dimensions of the cork would increase gradually until the cork meets up with the lid, at which point the dimensions would be about equal to the dimensions of the entrance of the tomb, so that the blocking stone would “seal” the tomb when the stone was pushed fully into the entrance of the tomb. I will use the decrease of four inches on each side (and the top) for the dimensions of the cork of a smaller blocking stone, and will use a decrease of six inches on each side (and the top) for the dimensions of the cork of a larger blocking stone.

The volume of the “cork” part of this smaller square blocking stone is a bit more tricky to figure out. The cork piece is not strictly a cuboid, because the dimensions of the end that goes into the tomb are smaller than the dimensions where it meets up with the lid. However, we can calculate the volume of a cuboid that has the larger dimension at the lid, and we can calculate the volume of a cuboid that has the smaller dimensions of the end that fits into the entrance, and then figure the average of those two volumes, in order to determine the volume of this unsymmetrical “cuboid”.

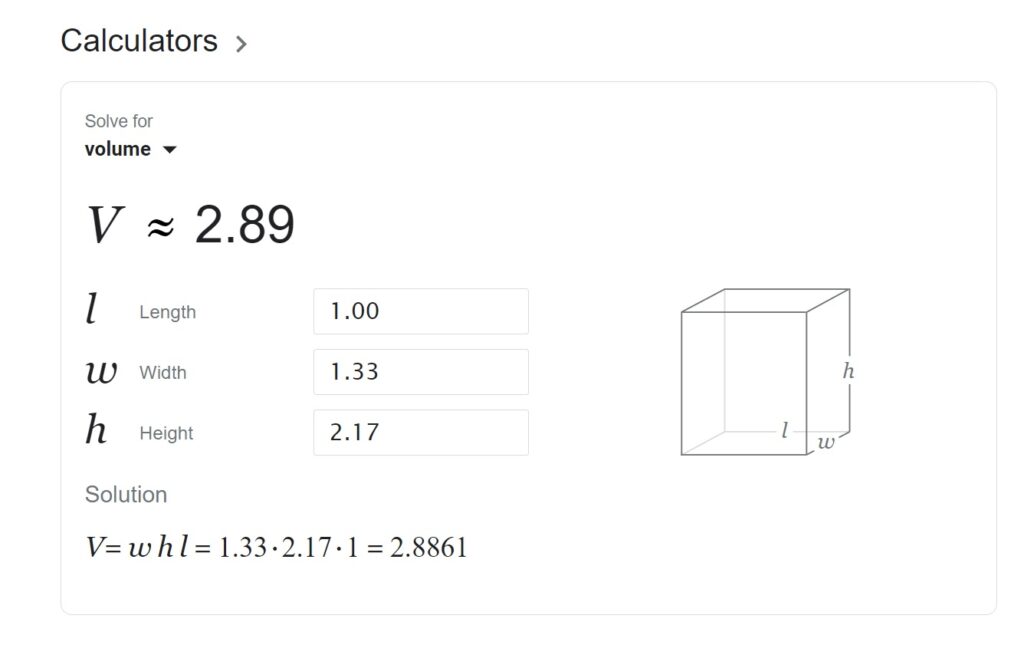
Volume of Cuboid with larger dimensions = 2.0 feet wide x 2.5 feet tall x 1.0 feet long = 5.0 cubic feet.

Volume of Cuboid with smaller dimensions = 2.0 feet wide minus 8 inches x 2.5 feet tall minus 4 inches x 1.0 feet long = 1.33 feet wide x 2.17 feet tall x 1.0 feet long = 2.89 cubic feet.

We now calculate the average of those two volumes to get the estimated volume of the cork of a smaller square blocking stone that would be large enough to block off a smaller-sized entrance to a stone tomb:

(5.0 cubic feet + 2.89 cubic feet) / 2 = 7.89 cubic feet / 2 = 3.95 cubic feet

We can now determine the estimated volume of a square blocking stone that would be large enough to block a smaller-sized entrance to a stone tomb by adding together the estimated volume of the lid of such a blocking stone with the estimated volume of the cork of such a blocking stone:

2.49 cubic feet (LID) + 3.95 cubic feet (CORK) = 6.44 cubic feet

THE WEIGHT OF A SMALLER SQUARE BLOCKING STONE

The weight of this smaller square blocking stone depends on what sort of rock it was made from.

• Limestone weighs 150 pounds/cubic foot
• Low-density Granite weighs 159 pounds/cubic foot
• High-density Granite weighs 180 pounds/cubic foot

Here are weight estimates based on likely types of stone used to make blocking stones:

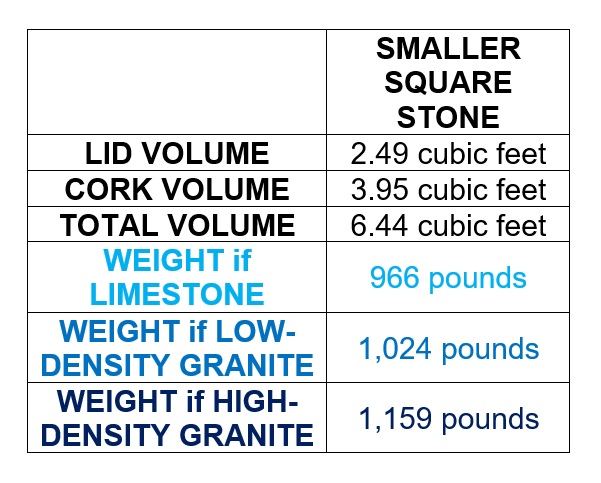
We may reasonably conclude that a square blocking stone that would be large enough to block a smaller-sized entrance to a stone tomb (i.e. 2.0 feet wide x 2.5 feet tall) would probably weigh between 960 pounds and 1,170 pounds.

Could just ONE PERSON (a healthy adult without a physical disability) move such a smaller square blocking stone away from the entrance to a stone tomb? In the next post of this series, I will argue that this is the case.