The question “Who moved the stone?” is used by Christian apologists to raise an objection against some skeptical theories about the alleged resurrection of Jesus, especially the Swoon Theory (see Objection #7 in Handbook of Christian Apologetics by Peter Kreeft and Ronald Tacelli, p.183-184), but also the Conspiracy Theory, and the Hallucination Theory.

In this post, I will argue that one healthy non-disabled adult can easily move a circular blocking stone that is the size and weight of the blocking stone used at the tomb of Jesus (assuming a circular blocking stone was used), contrary to the claims of many Christian apologists.

In Part 1 of this series, I showed that if a circular stone was used to block the entrance of Jesus’ tomb, that stone would probably have been between at least 3.2 feet in diameter (and 10 inches thick) and at least 4.0 feet in diameter (and 12 inches thick), depending on whether the entrance of the tomb was smaller or larger in size.

The weight of the stone depends on its size (volume) and the density of the stone from which it was composed. Here is a table with the various possible weights of a smaller (3.2 feet diameter, 10 inches thick) circular blocking stone and a larger (4.0 feet diameter, 12 inches thick) circular blocking stone:

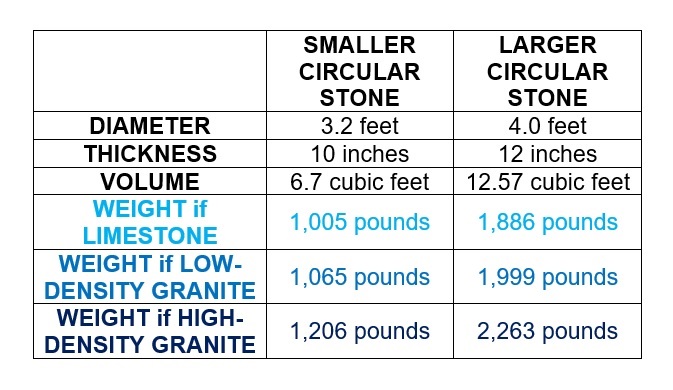
Based on these calculations, a circular blocking stone at the tomb of Jesus would probably have weighed between 1,000 pounds and 2,300 pounds.

In Part 1 of this series, I argued that just one healthy non-disabled adult could easily move a circular stone that weighed between 1,000 pounds and 2,300 pounds, because such a stone would constitute a WHEEL, and because WHEELS make it easy to move objects that are very heavy.

For example, I can EASILY push and move my 3,500-pound car (a 2015 Ford Escape SUV) by myself for several feet in less than one minute.

Another example is a world record that was set by a strong man named Kevin Fast in 2009. Kevin pulled an airplane weighing 208 TONS for 28 feet in under two minutes (because the aircraft was on wheels):

https://www.guinnessworldrecords.com/world-records/heaviest-aircraft-pulled-by-a-man

For these reasons, I am certain that I (or any other healthy adult who was not disabled or handicapped) could move a circular stone (shaped like a wheel) that was 4.0 feet in diameter and 12 inches thick, and that weighed 2,300 pounds for two feet in less than a minute without any serious effort or difficulty.

FURTHER EVIDENCE FROM ROLLING-RESISTANCE PRINCIPLES AND CALCULATIONS

The amount of effort required to move a heavy object on wheels (or on one wheel) can be calculated, and I will now show that such calculations and the relevant rolling-resistance principles clearly support the above conclusion that I arrived at on the basis of examples in which WHEELS allow just one person to move very heavy objects.

An object in motion tends to stay in motion. If you are driving down the freeway at 60 miles per hour, and you take your foot off the gas, your car will not immediately stop moving. If the freeway is roughly level, you will continue to move down the road at nearly 60 miles per hour. But your car will begin to lose speed, and it will slow down to 50 miles an hour, and then it will continue to slow down to 40 miles an hour, and if the freeway stays level, your car will eventually come to a complete stop. If there was no resistance to your car moving down the freeway, then it would continue to go forward at 60 miles per hour forever. Your car slows down because there is resistance to the forward motion of the car.

The car has to push through air, so there is some resistance to the forward movement of the car from the air. More importantly, there is resistance to the forward movement of the car from the wheels rolling on the road. How much rolling resistance there is depends on a few key factors:

• the diameter of the wheels
• the material the wheels are made of (i.e how soft or hard the wheels are)
• the material that the road is made of (i.e. how soft or hard the material is)
• the weight of the vehicle

The LARGER the diameter of the wheels, the LESS rolling resistance there will be. Double the diameter of the wheels and that will cut the rolling resistance in half.

The LARGER the weight of the vehicle, the MORE rolling resistance there will be. Double the weight of the vehicle and that will double the rolling resistance.

The HARDER the wheels are, the LESS rolling resistance there will be.

The HARDER the road or rolling surface is, the LESS rolling resistance there will be.

For example, there is much less rolling resistance (pound-for-pound) when moving heavy objects by train than there is when moving heavy objects by trucks that have rubber tires that ride on asphalt roads. Trains have wheels made of steel that ride on rails that are also made of steel. So, train wheels are very HARD, and the surface they roll on is also very HARD. The rolling resistance of a train is about one-tenth of the rolling resistance of a car that has rubber tires that roll on an asphalt road, for the same amount of weight.

A wheel made out of stone is clearly HARDER than a wheel made out of rubber. But a wheel made out of stone is not as hard as the steel wheels on a train. Thus, in terms of that factor, a wheel made of stone has LESS rolling resistance than a rubber tire but MORE rolling resistance than a wheel made of steel.

A circular blocking stone rolled in a groove or track just outside the entrance to the tomb. The surface that these stones rolled on was itself made of stone. The rolling surface for a circular blocking stone was HARDER than an asphalt road, but not as hard as the steel rails that train wheels roll on. Thus, in terms of that factor, a circular stone had LESS rolling resistance than tires rolling on asphalt but MORE rolling resistance than steel train wheels rolling on steel rails.

What about the diameter of wheels on a car and wheels on a train vs. the diameter of a circular blocking stone? The diameter of most wheels on a car range from about 25 inches to 33 inches (roughly from 2.0 feet to 2.8 feet). The standard diameter for a train wheel is 36 inches or 3.0 feet (see Wikipedia article “Train Wheel“). The smaller size of a circular blocking stone in Jerusalem in Jesus’ time would have been at least 3.2 feet in diameter, and a larger circular blocking stone would have been at least 4.0 feet in diameter. So, a smaller circular blocking stone would constitute a wheel that is larger than most car wheels, and only slightly larger than most train wheels. A larger circular blocking stone with a diameter of 4.0 feet has a significantly larger diameter than either a car wheel or a train wheel.

Thus, a smaller circular blocking stone would have a little LESS rolling resistance than a stone wheel that was the size of a car wheel or train wheel, and a larger circular blocking stone would have significantly LESS rolling resistance than a stone wheel that was the size of a car wheel or train wheel.

In relation to three factors (diameter, hardness of wheel, hardness of rolling surface) of the four main factors that determine rolling resistance, a circular blocking stone on a stone surface has LESS rolling resistance than a rubber car wheel on an asphalt road.

In terms of the weight factor, we can calculate rolling resistance for rubber tires on asphalt road as well as for steel train wheels on steel rails based on the maximum likely weight of the larger circular blocking stone: 2,300 pounds.

How much force does it take to keep a car weighing 2,300 pounds rolling on a level asphalt road? Here is a calculator that provides the answer to that question:

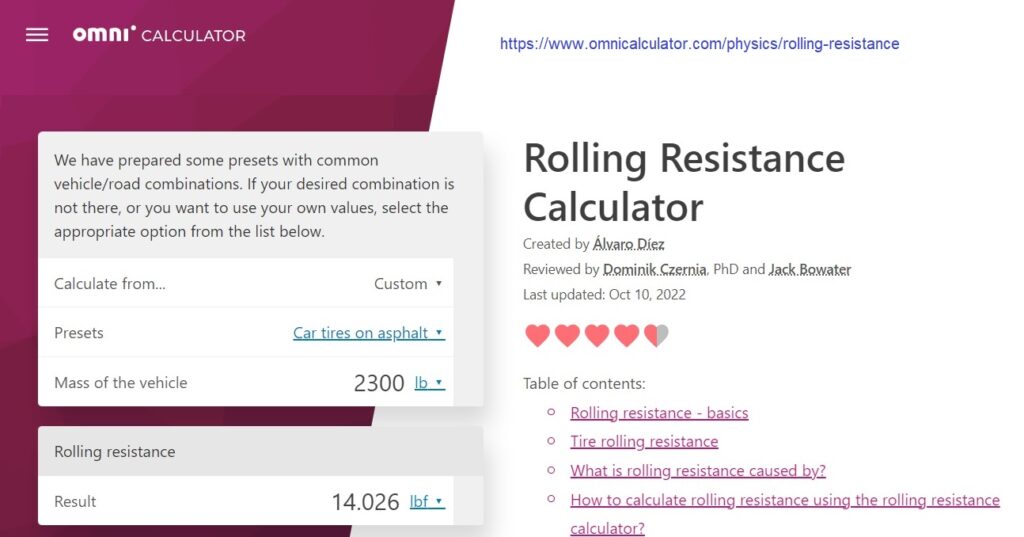
It only takes about 14 pounds of force to keep a 2,300 pound car with rubber tires rolling on a level asphalt road. I can push with at least 90 pounds of force against a wall, so this calculation shows why I am able to EASILY push my car (weighing 3,500 pounds) for a few feet on level asphalt in less than one minute.

It is even EASIER to keep 2,300 pounds rolling forward with steel train wheels on steel rails:

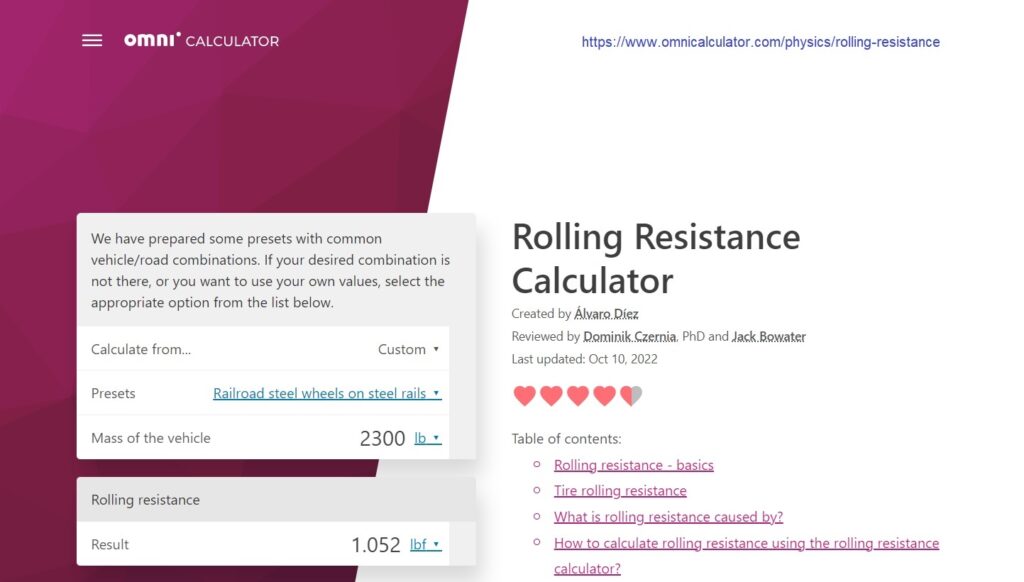
It only takes ONE POUND of force to keep 2,300 pounds rolling forward with steel train wheels on steel rails.

How much force would it take to keep a 4.0-foot diameter circular blocking stone weighing 2,300 pounds rolling on a stone surface? It would take LESS force than to keep 2.5-foot diameter rubber car tires on a car weighing 2,300 pounds rolling on a level asphalt road. Thus, it would take LESS THAN 14 pounds of force to keep a 4.0-foot diameter circular blocking stone weighing 2,300 pounds rolling on a stone surface.

Because steel train wheels are harder than a stone wheel, and because steel rails are harder than a stone path, the force required to keep a 2,300 pound circular blocking stone rolling on a stone path is probably GREATER than the force required to keep 2,300 pounds of stuff moving on steel train wheels that are rolling on steel rails (even though the blocking stone has a larger diameter than the train wheels). Thus, the amount of force required to keep a 2,300 pound circular blocking stone rolling on a stone surface is probably GREATER than just ONE POUND of force.

We can reasonably conclude that the force required to keep a 2,300-pound circular blocking stone rolling on a stone path is MORE THAN 1 pound but LESS THAN 14 pounds. Thus, a reasonable estimate is that it would take about 10 pounds of force to keep a 2,300-pound, 4.0-foot diameter circular blocking stone rolling on a stone path. Since I can push with a force of at least 90 pounds against a wall, this calculation confirms that I could EASILY generate enough force to keep such a circular blocking stone rolling.

There is one more point, however, to consider here. It takes GREATER force to get a heavy object on wheels to START rolling than it does to KEEP it rolling once it is in motion. How much more force would be required to get a 2,300 pound, 4.0-foot diameter circular blocking stone to START rolling as compared with the measly 10 pounds of force required to KEEP it rolling?

I don’t know how to calculate this in a precise way, but I do know a rule-of-thumb that can be used to estimate the additional force required to get a heavy object on wheels to START rolling:

Let’s use the larger figure of 2.5 times the sustaining force. We have estimated that to sustain the rolling of a 2,300 pound, 4.0-foot diameter circular blocking stone we need to apply about 10 pounds of force. 2.5 times 10 pounds = 25 pounds. Therefore, in order to START the rolling of a 2,300 pound, 4.0-foot diameter circular blocking stone we would need an initial force of 25 pounds, which could quickly be reduced to about 10 pounds of force.

Since I can push with at least 90 pounds of force against a wall, I could EASILY provide the 25 pounds of force required to START the rolling of a larger circular blocking stone (weighing 2,300 pounds with a diameter of 4.0 feet), and I could VERY EASILY provide the measly 10 pounds of force required to KEEP that circular blocking stone moving.

Therefore, based on the principles and calculations relevant to rolling resistance, I have provided further confirmation that any healthy adult who is not disabled would be able to move even a larger circular blocking stone from the entrance to the tomb of Jesus all by himself (or herself).

ONE LAST EXAMPLE SHOWING HOW EASY IT IS TO ROLL A HEAVY WHEEL

One strong-man competition that is relevant to this subject is tire flipping. Here is a video of a tire-flipping contest: https://youtu.be/6PWTWamUMyc

Tire flipping, however, is clearly harder to do than simply rolling a heavy tire. But I found a YouTube video with a man giving advice to people who want to enter tire-flipping contests, and that video includes two scenes where the man giving the advice ROLLS a 1,000-pound tire on asphalt, and it is clearly VERY EASY for him to do this.

Watch the video below from 2:20 to 2:25 and also from 3:05 to 3:25, and you will see that it requires very little effort for one person to roll a 1,000-pound tire on asphalt:

https://youtu.be/smfrCzHgYRI

Remember that a stone wheel is HARDER than a rubber wheel and that a stone path is HARDER than an asphalt surface. So, a 1,000-pound stone wheel on a stone surface has LESS rolling resistance than a 1,000-pound rubber tire on an asphalt surface (for wheels of the same diameter). Since the tire in the video appears to be about 5 feet in diameter, we can infer that a 5-foot diameter stone wheel that weighs 1,000 pounds and is rolled on a stone surface will be EVEN EASIER to roll than rolling this 1,000-pound rubber tire on an asphalt surface.