When drinking alcoholic beverages it is good to know how much alcohol one is consuming, especially if one needs to drive home after having such beverages.

Beer has less alcohol than wine, and wine has less alcohol than liquor.  Beer commonly ranges from 4% to 6% alcohol by volume (ABV).  Wine commonly ranges from 8% to 14% ABV,  and liquor commonly ranges from 30% to 60% ABV.

In the USA, a standard drink has .6 oz of alcohol:

• One 12 0z bottle of beer that is 5% alcohol by volume has  .6 oz of alcohol  (.05 x 12 oz = .6 oz).
• One 5 oz glass of wine that is 12% alcohol by volume has  .6 oz of alcohol (.12 x 5 oz = .6 oz).
• One 1.5 oz shot of 80 proof whiskey  is 40% alcohol by volume and has  .6 oz of alcohol  (.40 x 1.5 oz = .6 oz ).

In terms of amount of alcohol contained per ounce of beverage, beer is weak, wine is moderate, and liquor is strong.  We can use the “standard drink” as a general guideline for consumption of alcoholic beverages.  One 12 oz beer has about as much alcohol as one 5 oz glass of wine, and about as much alcohol as one 1.5 oz shot of 80 proof whiskey (such as Jack Daniel’s).

Inductive arguments also come in different stengths: weak, moderate, and strong.  As we saw in the previous post in this series, Swinburne’s primary objection to Plantinga’s dwindling probabilities argument focuses on the point that there can be more than one way or route to get to a conclusion or hypothesis and that to arrive at a fully accurate probability of an hypothesis, one must take into consideration all of the various ways or routes that contribute to the probability of the hypothesis.

Another way of making this point is that there can be mutliple inductive reasons or arguments for the same conclusion.  When there are multiple inductive reasons for the same conclusion, the probability of the conclusion can exceed the probability conferred upon it by any one of the reasons given to support it.  In other words, with inductive reasoning, it is possible to provide solid support for a conclusion by means of ONE STRONG inductive reason or by means of a FEW MODERATE inductive reasons, or by means of MANY WEAK inductive reasons or arguments.  One can get drunk by consuming a six-pack of 12 oz beers, just as one can get drunk by consuming a single 9 oz glass of 80 proof whiskey.

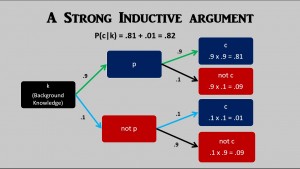
With inductive reasoning, the inferences are less than certain, and we can express the degree of uncertainty in terms of probability.  Furthermore, with inductive arguments that have empirical premises, the premises are often less than certain, and we can express the degree of uncertainty in terms of probability.  A probability of .9 is a high probability, so an inductive argument that had a premise the truth of which had a probability of .9, and an inference the probability of which was also .9 would be a paradigm case of a STRONG inductive argument (click on image to see diagram more clearly):

p therefore c.

It is tempting to simply multiply the probability of the premise being true (.9) times the probability of the conclusion being true given that the premise is true (.9) in order to get the probability of the conclusion (.81).  But this neglects the alterntaive path where the premise is false (not p).  Even if the premise is false, there can still be some degree of probability that the conclusion will be true.  I made this probability small (.1) so that the truth of the premise makes a big difference.  If the conclusion had a probability of .9 whether the premise was true or not, then the truth of the premise wouldn’t matter.  In a strong inductive argument, we expect the truth of the premise to make a big difference.

So, this paradigm case of a STRONG inductive argument confers a probability of .82  on its conclusion.  This is very close to the probability of rolling one die just once and the die coming up any number other than six (1, 2, 3, 4, or 5).  There are five chances in six that a number other than six will come up when rolling one die just once:  5/6 = .8333 or approximately: .83.  So, we can get a good feel for the probability involved in this paradigm case of a strong inductive argument by means of the analogy with the probability of rolling one die just once and the die coming up any number other than six.

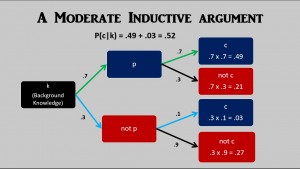
If we lower the probability of the truth of the premise to .7 and also lower the probability of the inference to .7, then we will have a paradigm case of a MODERATE inductive argument (click on image to see diagram more clearly):

Again, it is tempting to simply multiply the probability of the truth of the premise (.7) times the probability of the truth of the conclusion given the truth of the premise (.7), and conclude that the probability of the conclusion is .49, but we need to also consider the probability of the conclusion in the case that the premise is false.  Once again I have assigned a small probability to this (.1) because with a good argument, we expect the truth of the premise to make a significant difference.  If the conclusion had a probabilty of .7 whether the premise was true or not, then the truth of the premise would not make any difference.

In this paradigm case of a MODERATE inductive argument, the probability of the conclusion comes out to be .52, which is very close to the probability of flipping a coin once and having the coin come up heads, and also very close to the probability of rolling one die once and the die coming up an even number (2, 4, or 6).  There are six possible outcomes when rolling a die once, and the die coming up an even number represents three of those six possible outcomes.  Since each outcome has an equal probability, the probability of coming up an even number is 3/6  =  .50.  So, we can get a good feel for the strength of such a MODERATE inductive argument based on our experience and understanding of the probabilty of flipping a coin and it coming up heads or of the probability of rolling one die and it coming up an even number.

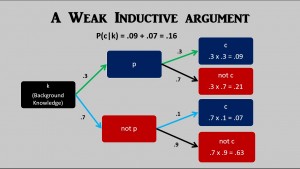
If we lower the probability of the premise down to .3  and also lower the probability of the inference to .3, then this will give us a paradigm case of a WEAK inductive argument(click on image to see diagram more clearly):

The probability of the conclusion of this paradigm case of a WEAK inductive argument is .16, which happens to be very close to the probability of rolling one die once and the die coming up as a six.  There are six different possible outcomes of rolling a die (1, 2, 3, 4, 5, or 6), and the die coming up as a six is just one outcome out of those six possible outcomes.  Since each outcome is equally probable, the probability that the die will come up as a six is 1/6 =  .1666 or approximately .17.  So, our experience and understanding of the probability of rolling one die once and it coming up a six gives us a good feel for the probability of the conclusion of this paradigm case of a WEAK inductive argument.

Just as one can get drunk either by consuming a six-pack of beer or by consuming one 9 oz glass of 80 proof whiskey, so one can make a solid inductive case for a claim either with many WEAK inductive arguments or with a few MODERATE inductive arguments or with just one STRONG inductive argument.  To get a feel for how many WEAK inductive arguments are required in order to have the equivalent force of one STRONG inductive argument, we can compare the probabilities of the above paradigm cases of WEAK and STRONG arguments, and use an analogy with the probability of rolling multiple dice to get a six compared to rolling one die just once to get any number other than a six.

Our paradigm case of a STRONG inductive argument gave the conclusion a probability of .82, which is very close to the probability of rolling one die once and it coming up as any number less than six (1, 2, 3, 4, or 5), which has a probability of about .83.  Our paradigm case of a WEAK inductive argument gave the conclusion a probability of .16, which is very close to the probability of rolling one die once and it coming up as a six, which has a probability of about .17.  If we had multiple independent WEAK inductive arguments for the conclusion, that would be analogous to rolling multiple dice to try to get at least one of the die to come up as a six.  How many dice would we need to roll to get to a probability of about .82 that at least one die would come up as a six?

If we roll nine dice, the probabilty of at least one die coming up as a six would be .8061934  or approximately .81, which is very close to the probability of the conclusion with our paradigm case of a STRONG inductive argument (.82).  Thus, if we have multiple WEAK inductive arguments that function independently of each other (where the truth of the premise of one argument has no significant impact on the probability of the truth of the premise of any of the other arguments and no significant impact on the probability of the inference in any of the other arguments), then we would need about nine such arguments in order to get the equivalent strength as our paradigm STRONG inductive argument.

With nine dice, there are 6⁹ possible outcomes. There are 5⁹ outcomes that include no sixes. Thus the probability of rolling nine dice and NOT getting at least one six is 5⁹/6⁹ = 1.953125/10.077696 = .1938066.

There are only two possible cases:

EITHER at least one die comes up as a six OR no die comes up as a six.

Thus if we add the probabilities of these two possible cases together, the sum would be 1.0. Thus, we can determine the probability of at least one die coming up as a six by subtracting the probability of the case where no die comes up a six from 1.0:

a: At least one die comes up as a six.

n: No die comes up as a six.

r: We roll nine dice just once.

P(a|r) + P(n|r) = 1.0

P(a|r) = 1.0 – P(n|r)

P(a|r) = 1.0 – .1938066

P(a|r) = .8061934 or approximately .81

How many arguments similar in strength to the paradigm case of a MODERATE inductive argument would be required in order to be about the same force as just one argument with the strength of our paradigm case of a STRONG inductive argument?  The conclusion of the paradigm case of a STRONG inductive argument has a probability of  .82, and the conclusion of the paradigm case MODERATE inductive argument has a probability of .52.  The probability of the conclusion in the case of the MODERATE argument is close to the probability of rolling one die just once and it coming up an even number (probability = .50).  So, how many dice would one need to roll in order to have a probability of about .82 of at least one die coming up an even number?

With just two dice we get close to the targeted probability of .82.  If you roll two dice, the probability that at least one die will come up as an even number is .75.  If you roll three dice, the probability that at least one die will come up an even number is .875.  So, rolling two dice is not quite enough, but rolling three dice is more than what is required.  Thus, to acheive a strength similar to just one of our paradigm STRONG inductive arguments, you need two or three arguments with a strength similar to the paradigm case of a MODERATE inductive argument (assuming that the arguments support the conclusion independently of each other).

When rolling two dice just once, there are 36 possible outcomes (6 x 6 = 36), and there are 18 outcomes with exactly one even number,  and there are 9 outcomes with exactly two even numbers.  So there are a total of 27 outcomes with at least one even number.  That means that the probability of rolling two dice just once and getting at least one die to come up as an even number is 27/36 = .75.

When rolling three dice just once, there are 216 possible outcomes (6 x 6 x6  = 216).  Cases of the desired outcome: (1) only the first die comes up even (3 x 3 x 3 = 27 outcomes), (2) only the second die come up even (3 x 3 x 3 = 27 outcomes), (3) only the third die comes up even (3 x 3 x 3 = 27 outcomes), (4) only the first and second dice come up even (3 x 3 x 3 = 27 outcomes), (5) only the first and third dice come up even (3 x 3 x 3 = 27 outcomes), (6) only the second and third dice come up even (3 x 3 x 3 = 27 outcomes), (7)  all three dice come up even (3 x 3 x 3 = 27 outcomes).  There are a total of 7 different cases each with 27 desired outcomes, so there is a total of 189 desired outcomes out of 216 possible outcomes.  The probability when rolling three dice just once that at least one die comes up an even number is thus 189/216 = .875 or approximately .88.

I realize that in the real world when we have multiple inductive arguments for the same conclusion, they will often NOT be independent from each other.  It will often be the case that the truth of one premise will have an impact on either the probability of some other premise in one of the other inductive arguments or on the probability of an inference in one of the other inductive arguments.  So, figuring out the probability of the conclusion in such cases will be more complex and more difficult than in cases in which multiple inductive arguments for the same conclusion function independently of each other.

However, thinking about and understanding the probability of the above paradigm cases of WEAK, MODERATE, and STRONG inductive arguments, and the analogies with the probability of various outcomes when rolling one die (WEAK: getting a six,  MODERATE: getting an even number, STRONG: getting any number less than a six), and the approximate equivalents between multiple WEAK or MODERATE inductive arguments and one STRONG inductive argument (assuming independence of multiple arguments) gives one a baseline starting point for dealing with inductive arguments.