Previously, I have only considered the very simple case where one person has a memory of having previously had a theistic religious experience (hereafter: TRE) of a generic sort–an experience in which it seemed (epistemically) to him/her that God was present.  There were a couple of basic points made about probable inferences in contrast to necessary or deductive inferences, but there are even more interesting points of logic and probability ahead as we consider more complex and more realistic scenarios.

For most skeptics, we don’t have religous experiences, and if and when we do have something that might be called a religious experience, we are not inclined to believe that the experience was caused by God or by any sort of supernatural person or being.  This might also be true for many Christians and Jews and Muslims.  In any case, there is a significant portion of the population for whom the evidence of religious experience must be second-hand and based on the testimony of others.

Recall that Swinburne proposes a principle concerning testimony which is similar to his principles about experience and memory:

TESTIMONY

…(in the absence of special considerations) the experiences of others are (probably) as they report them. (EOG, p.322) 

So for many of us, especially for us skeptics, doubters, and atheists, there is a longer chain of probable inferences requried to come to a conclusion about the existence of God.  Furthermore, since testimony about TREs is not a constant feature of our experiences, once such a testimony is given and heard, the force of that testimony remains only by means of memories of having heard (or read) that testimony.  Thus, for many people, and probably for most skeptics, there are number of steps of probable inferences in reasoning to  a conclusion about the probability of God on the basis of an alleged TRE:

1. It seems (epistemically) to me that I heard John testify last Sunday to having had a generic TRE when he was hiking in Yosemite last summer.

2. There are no special considerations casting doubt on my apparent memory about John testifying about having had a TRE.

3. If it seems to a subject that in the past he perceived something  or did something, then (in the absence of special considerations), probably he did. [Swinburne’s principle concerning memory]

Therefore:

4. It is probably the case that John testified last Sunday to having had a generic TRE when he was hiking in Yosemite last summer.

5. There are no special considerations casting doubt on John’s honesty and integrity.

6. If someone testifies to having had a certain experience on a certain occasion in the past, and if there are no special considerations casting doubt on that person’s honesty and integrity, then it is probably the case that it seemed (epistemically) to that person during his/her testimony that he/she had that experience on that occasion in the past. [This is an additional principle in the spirit of Swinburne’s other principles]

Therefore:

7.  It is somewhat probable (it is probable that it is probable) that at the time John was giving his testimony it seemed (epistemically) to John that he had had a generic TRE when he was hiking in Yosemite last summer.

8.  There are no special considerations casting doubt on the veridicality or reliability of John’s apparent memory about a religious experience while he was hiking in Yosemite last summer.

9. If it seems to a subject that in the past he perceived something  or did something, then (in the absence of special considerations), probably he did. [Swinburne’s principle concerning memory]

Therefore:

10.  It is probable that it is probable that it is probable that John had a generic TRE when he was hiking in Yosemite last summer.

11. There are no special considerations casting doubt on the veridicality or reliability of this generic TRE had by John.

12. In the absence of special considerations casting doubt on the veridicality or reliabilty  of the experience, if it seems (epistemically) to a subject that x is present (and has some characteristic), then probably x is present (and has that characteristic). [Swinburne’s principle of experience]

Therefore:

13. It is probable that it is probable that it is probable that it is probable that God was present with John during his generic TRE when he was hiking in Yosemite last summer.

Because a chain consisting of a number of probable inferences is required to get from that actual data (my apparent memory of John giving testimony) to the conclusion (about God being present with John during a religious experience), the probability is somewhat diminished.  Suppose that we interpret “probable” to mean having a probability of about .6.   In that case the chain of four probable inferences requires that we multiply this probability four times:

.6 x .6 x .6 x .6

= .36 x .36

= .1296

If we round this to a single significant figure, then the probability of God’s existence, based on this specific evidence and Swinburne’s principles, would be: .1  or one chance in ten.  Not a very impressive conclusion.

Furthermore, we are assuming that the premises that state there are no special considerations casting doubt (on the testimony, or memory, or experience) are certain.  But we are finite and fallible human beings, so those premises might add more uncertainty into the equation, and reduce the probability further.  And we also may be less than certain about the various epistemological principles, so that could further reduce the probability of the conclusion.

However, if we make the simplifying assumption that the veridicality of each generic theistic religious experience is independent of the veridicality of other generic theistic religious experiences, then because there is a great deal of testimony about a great many alleged generic theistic religious experiences, even a very modest probability of veridicality will be sufficient to show that it is virtually certain that God exists.  If you roll two dice a hundred times, you are very likely to come up with a pair of sixes on one of the rolls, even though it is unlikely that you will get a pair of sixes on any specific given roll.  Similarly, if each and every generic theistic religious experience has some small but significant chance of being veridical, then if a hundred such experiences occur, it is virtually certain that at least one would be veridical (i.e. God would in fact be present with the experiencer).

Let’s set aside that issue of the chain of probable inferences involved in a memory of a testimony about a religious experience.  Let’s assume that we have some way to be confident that a number of generic theistic relgious experiences have occurred.  Let’s assume that with the examples we have collected there are no special considerations casting doubt on the veridicality of the experiences, and that the veridicality of each generic theistic religious experience was independent of the veridicality of other such experiences. Let’s assume, therefore, that each generic theistic religious experience has a probability of .6 of being veridical (meaning that God was actually present and being experienced by the believer).

[It is important to note here that Swinburne thinks that the veridicality of a generic TRE is NOT independent of the veridicality of other generic TREs.  Furthermore, I agree that the veridicality of a generic TRE is NOT independent of the veridicality of other generic TREs.  However, it is still worth considering the idea of them being independent, partly because this is a simplifying assumption making probability calculations simpler, but also just to be a bit clearer about the importance and implications of dependence relationships between TREs by means of contrast with the idea of TREs being independent of each other (in terms of veridicality).]

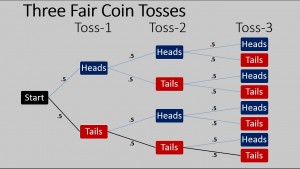
Consider the paralell scenario of fair tosses of a coin, where the probability of getting heads is .5 and the probability of tails is also .5.  If you do three fair tosses, what is the probability that at least one toss would come up heads?  We know that EITHER at least one toss will come up heads OR no toss will come up heads.  Those are the only two possibilities.  So, it is certain that one or the other of those possibilities will be realized if we toss the coin three times:

O: At least one toss comes up heads.

N: No toss comes up heads.

E: Every toss comes up tails.

====================

15. Either O or N.    [This is an analytic truth; we know with certainty that this statement is true.]

16. A statement that is known with certainty to be true has a probability of 1.0.

Therefore:

17. P(O or N) =  1.0   [The probability that either O or N will occur EQUALS 1.0, i.e. this is certain.]

 18. The probability of a disjunction is equal to the sum of the probabilities of each disjunct minus the probability of both disjuncts being true.

Therefore:  

19. P(O) + P(N) – P(O and N) = 1.0    [The probability that O occurs PLUS the probability that N occurs MINUS the probability that both O and N occur EQUALS 1.0.]

20. If O occurs, then N does not occur, AND if N occurs, then O does not occur.  [O and N are mutually exclusive outcomes.]

Therefore:

21. ~(O and N)   [O and N are mutually exclusive outcomes, so we know with certainty that they cannot both occur.]

22. If we know with certainty that a statement is NOT the case, then the probability of that statement is zero.

Therefore:   

23. P(O and N) = 0   [The probability that both O occurs and N occurs EQUALS zero.]

24.  If  two expressions are equivalent, then we can replace one expression with the other in any equation. 

Therefore:

25. P(O) + P(N) – 0 = 1.0   [The probabilty that O occurs PLUS the probability that N occurs MINUS 0 EQUALS 1.0.]

26. x – 0 = x   [Any number minus zero equals that number.]

Therefore:

27:  P(N) – 0 = P(N)

Therefore:

28.  P(N) can be substituted in any equation for the expression P(N) – 0.

Therefore:

29. P(O) + P(N) = 1.0   

30.  We can subtract the same thing from both sides of a true equation to produce a true equation.

Therefore:

31. P(O) = 1.0 –  P(N)   [The probability that O occurs EQUALS  1.0 MINUS the probability that N occurs.]

32. P(N) = P(E)   [The probability that no toss comes up heads is the same as the probability that every toss comes up tails.]

33. If they are equal, then we can substitute P(E) for P(N) in any true equation to produce another true equation.

Therefore:

34. P(O) = 1.0 – P(E)    [The probability that O occurs EQUALS 1.0 MINUS the probabilty that E occurs.]

That is a lot of work for this meager conclusion:

The probability that at least one toss comes up heads EQUALS 1.0 MINUS the probability that every toss comes up tails.

But it is easy to figure out the probability that every toss comes up tails.  Let’s start with the scenario where we do three (fair) coin tosses:

In order to come up with tails on all three tosses, one must come up with tails on the first toss (probability = .5) and then come up with tails on the second toss (probability = .5) and then come up with tails on the third toss (probability = .5).  So, the probability of coming up with tails on all three tosses is:

.5 x .5 x .5

= .25 x .5

= .125

P(E) = .125   (or .1 rounded to one significant figure).

We have determined that the probability of coming up with heads at least once is equal to 1.0 MINUS the probability of coming up tails on all three tosses:

P(O) =  1.0 – P(E)

Therefore:

P(O) = 1.0 – .125

Therefore:

P(O) = .875  (or .9 rounded to one significant figure)

So, it is very probable that in three (fair) tosses of a coin, that heads will come up at least one time.

What if we do six (fair) tosses of a coin?  What is the probability that heads will come up at least once?  The same logic applies.  The probability that heads will come up at least once EQUALS 1.0 MINUS the probability that tails will come up on every toss:

P(O) = 1.0 – P(E)

The only significant difference is that it is much less likely for tails to come up six times in a row, as compared with tails coming up three times in a row.  In order to come up with tails on all six tosses, the first toss must come up tails (probability = .5), the second toss must also come up tails (probability = .5), etc.  Thus the probability that tails will come up every time in six (fair) tosses of a coin is:

.5 x .5 x .5 x .5 x .5 x .5

=  .25 x .25 x .25

= .015625  [I will round off when calculation is completed.]

Therefore (in the case of six fair tosses):

P(O) = 1.0 – .015625

P(O) = .984375  (rounded to two significant figures: .98 , and rounded to one significant figure: 1)

We can see that with just six tosses of a coin it become highly probable, nearly certain, that at least one toss will come up heads.  We can reasonably conclude that the probability of heads coming up at least once in six fair tosses of a coin is greater than .9 but  less than 1.0:

.9 < P(O) < 1.0

The same logic and similar math applies to analogous scenarios with TREs, where we consider having evidence consisting of a set of three TREs and then consider having evidence consisting of a set of six TREs, given the simplifying assumption that the veridicality of a TRE is independent of the veridicality of other TREs.

Let’s re-define the basic statements abbreviated by the letters used in reasoning about coin tosses:

O:  At least one of the TREs is veridical (i.e. is the result of God actually being present).

N: None of the TREs is veridical.

E:  Every one of the TREs is non-veridical.

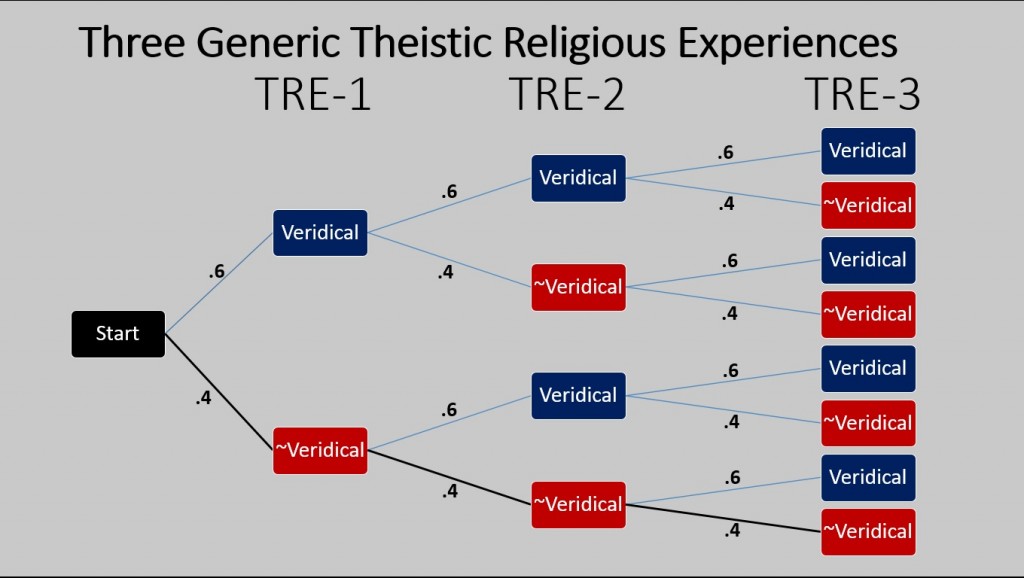
Suppose we have accepted three generic TREs as having no special considerations casting doubt on their reliability or veridicality.  Suppose that we take each one of the TREs to be probably veridical, meaning that there is a probability of .6 that the TRE is veridical.  Suppose we assume that the veridicality of any one TRE is independent of the veridicality of the other TREs.  We can represent this with a probability tree diagram that is very similar to the above tree diagram for coin tosses:

In this case we can apply the previous formula:

P(O) =  1.0 – P(E)

First, let’s determine the value of P(E), the probability that every one of the three TREs is non-veridical.  In order for all three of a series of three TREs to be non-verdical, the first TRE must be non-veridical (probability = .4, because the probabiliy of it being veridical is .6), and then the second TRE must also be non-veridical (probability = .4), and the third TRE must be non-veridical (probability = .4).  Thus, the probability that all three TREs in the series will be non-veridical is:

.4 x .4 x .4

= .16 x .4

= .064  [I will round after calculation is completed]

Therefore:

P(E) = .064

Therefore:

P(O) =  1.0 – .064

P(O) = .936  (or rounded to one signigicant figure: .9)

Thus, with just three “clean” (having no special considerations casting doubt on them)  generic TREs as evidence, the probability that at least one of them is veridical (i.e. is the result of God actually being present) is high, about .9.

What if we had six clean generic TREs as our evidence?  The probability that EVERY one of the six TREs was non-veridical would be this:

.4 x .4 x .4 x .4 x .4 x .4

= .16 x .16 x .16

= .004096  [I will round number when calculation is completed.]

Therefore:

P(E) = .004096

P(O) = 1.0 – P(E)

Therefore:

P(O) = 1.0 – .004096

P(O) = .995904  ( or approximately: 1.0)

With just six clean generic TREs, the probability (based on the various assumptions above) that at least one of these TREs was veridical (i.e. the result of God actually being present during the experience) would be about .99, nearly 1.0,  nearly certain.

To be continued…